|
[Magnetic field lines around a rectilinear current] ![\includegraphics[width=.4\textwidth]{Bilder/gerader-leiter}](img51.png) [Magnetic field at point
[Magnetic field at point ![\includegraphics[width=.52\textwidth]{Bilder/gerader-leiter2}](img52.png)
|
This section is an introduction to the theory of the magnetic field around a current carrying conducting line and the forces acting on a magnetic marker inside the produced magnetic gradient field. Additionally, some basic ideas about the manipulation and positioning of a magnetic markers with conducting lines will be discussed.
|
[Magnetic field lines around a rectilinear current] ![\includegraphics[width=.4\textwidth]{Bilder/gerader-leiter}](img51.png) [Magnetic field at point
[Magnetic field at point ![\includegraphics[width=.52\textwidth]{Bilder/gerader-leiter2}](img52.png)
|
A straight current generates a magnetic field that is inverse
proportional to the radius ![]() . The field lines are concentric
circles orthogonal to the straight current, see figure
1.9(a). To calculate the magnetic field of a
straight current we start from the Ampère-Laplace law:
. The field lines are concentric
circles orthogonal to the straight current, see figure
1.9(a). To calculate the magnetic field of a
straight current we start from the Ampère-Laplace law:
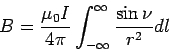 |
(1.3) |
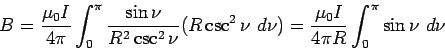 |
(1.4) |
After we can calculate the magnetic field ![]() at every point around a
long and thin conducting line, we also want to set a superparamagnetic
marker inside this magnetic field and calculate the acting forces.
at every point around a
long and thin conducting line, we also want to set a superparamagnetic
marker inside this magnetic field and calculate the acting forces.
0.5
![\includegraphics[width=.5\textwidth]{Bilder/theoretical-setup}](img76.png)
|
Figure 1.10 shows a simplistic setup
for a magnetic particle on a surface near a conducting line. When we
neglect different heights of the center of the magnetic particle and the
center of the conducting line, this is only a two-dimensional problem.
While the current flows in-plane
through the conducting
line, the magnetic field is always perpendicular to the plane and so it
is easy to calculate the magnetic field for every point in the plane.
When the current is turned on in this simple setup, a magnetic field is
generated that affects the magnetic particle. In the case of
ferromagnetic markers with large anisotropy, the markers would start to
rotate in order to align themselves to the magnetic field, as the dipole
wants to go into the state of minimal energy [29]. The
magnetic torque forced on the marker is
![]() .
.
But in this thesis, only superparamagnetic markers were used. The
ferromagnetic crystallites inside the core of the markers are so small
(![]() 1-10nm) that they show superparamagnetic behaviour. In such
small crystallites, the thermal energy is sufficient to change the
direction of the magnetisation, so the overall magnetic moment averages
to zero. Therefore, the crystallite exhibits a behaviour similar to
paramagnetism, where the magnetic moment
1-10nm) that they show superparamagnetic behaviour. In such
small crystallites, the thermal energy is sufficient to change the
direction of the magnetisation, so the overall magnetic moment averages
to zero. Therefore, the crystallite exhibits a behaviour similar to
paramagnetism, where the magnetic moment ![]() follows the langevin
equation:
follows the langevin
equation:
The change of the magnetic moment of the markers is very small for the
applied outer fields. Therefore, it is only a small error when we assume
the marker as a constant magnetic dipole for the bond-force measurements
(see chapter 4). The force exerted on the marker can
then be written as [71]:
| (1.9) |
To hold a particle in a specified position, a trap must be build with
the magnetic fields. But according to EARNSHAWS
theorem, it is not possible to build a trap with any
combinations of outer magnetic fields. SAMUEL EARNSHAW already
proved in 1842 [36] that if inverse-square-law forces,
such as the magnetic force
![]() , govern a group of
charged particles, they can never be in stable equilibrium. The reason
for this is that inverse-square-law forces follow the Laplace partial
differential equation, and the solution of this equation does not have
any local maxima or minima. There are only saddle-type equilibrium
points, instead. Although not applicable for the experiments in this
thesis, in principle one can circumvent Earnshaw's theorem by using
time-varying fields, active-feedback systems, diamagnetic systems
(extremely low forces) or superconductors.
, govern a group of
charged particles, they can never be in stable equilibrium. The reason
for this is that inverse-square-law forces follow the Laplace partial
differential equation, and the solution of this equation does not have
any local maxima or minima. There are only saddle-type equilibrium
points, instead. Although not applicable for the experiments in this
thesis, in principle one can circumvent Earnshaw's theorem by using
time-varying fields, active-feedback systems, diamagnetic systems
(extremely low forces) or superconductors.
Naturally one would like to guide a particle between the conducting lines that create the magnetic field. But this is only possible for particles that follow the magnetic gradient to local minima. This was e.g. done by DEKKER et al. [30] to guide neutral atoms on a chip. But the magnetic particles used in this thesis follow the magnetic gradient to the local maxima, and the local maxima are always at the edges and in the corners of the conducting lines.
So, in the experiments in this thesis, we trapped particles at the crossing of two conducting lines or in a corner (see chapters 3 and 5).